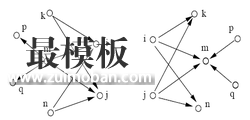
本文介绍HITS算法在Web挖掘中的优化与改进。
将查询q提交给基于关键字查询的检索系统,从返回结果页面的集合总取前n个网页(如n=200),作为根集合(root set),记为S,则S满足: 1.S中的网页数量较少 2.S中的网页是与查询q相关的网页 3.S中的网页包含较多的权威(Authority)网页 通过向S中加入被S引用的网页和引用S的网页,将S扩展成一个更大的集合T.以T中的Hub网页为顶点集V1 ,以权威网页为顶点集V2 。 V1中的网页到V2中的网页的超链接为边集E,形成一个二分有向图.对V1中的任一个顶点v,用h (v) 表示网页v的Hub值,且h (v)收敛;对V2中的顶点u,用a ( u) 表示网页的Authority值。 开始时h (v)=a(u)=1,对u执行I操作,修改它的a(u),对v执行O操作,修改它的h(v),然后规范化a (u)Ph (v) ,如此不断的重复计算下面的I操作和O操作,直到a (u) 。 其中I操作:a(u) = Σh(v) ;O操作: h(v) = Σa (u) 。每次迭代对a(u) 、h(v) 进行规范化处理:a(u)=a(u)PΣ[a(q)]2;h(v) = h(v)PΣ[h(q)]2 。 HITS算法目前存在一些不足:(1)、偏离查询主题。如果在扩展网页集合里包含部分与查询主题无关的页面,而且这些页面之间有较多的相互链接指向,那么使用HITS算法很可能会给予这些无关网页很高的排名,造成查询结果偏离查询主题。(2)、结构不稳定,在原有的“扩充网页集合”内,如果添加删除个别网页或者改变少数链接关系,则HITS算法的排名结果就会有非常大的改变。(3)、计算效率较低,因为HITS算法是与查询相关的算法,所以必须在接收到用户查询后实时进行计算,而HITS算法本身需要进行很多轮迭代计算才能获得最终结果,这导致其计算效率较低。 二、HITS 算法的优化与改进 1、改进方法 文章认为页面的权威性和中枢性 的计算不仅要考虑累计链接数量,也应考虑网页的链接增幅。这样能够帮助新发布页面和受关注的页面更快地进入用户视 野,提高查询的精确度。authority和hub值的更新不应仅仅根据优先情结决定的累积链接数量计算,还要考虑到网页的增长程度。本文使用引用增幅表示单个网页的增长,提出一种混合页面内容分析和网页引用增幅的HITS算法。 2、具体算法 import networkx as nx G=nx.path_graph(4) h,a=nx.hits(G) hits的python源代码
def hits(G,max_iter=100,tol=1.0e-8,nstart=None,normalized=True):
"""Return HITS hubs and authorities values for nodes.
The HITS algorithm computes two numbers for a node.
Authorities estimates the node value based on the incoming links.
Hubs estimates the node value based on outgoing links.
Parameters
----------
G : graph
A NetworkX graph
max_iter : interger, optional
Maximum number of iterations in power method.
tol : float, optional
Error tolerance used to check convergence in power method iteration.
nstart : dictionary, optional
Starting value of each node for power method iteration.
normalized : bool (default=True)
Normalize results by the sum of all of the values.
Returns
-------
(hubs,authorities) : two-tuple of dictionaries
Two dictionaries keyed by node containing the hub and authority
values.
Examples
--------
>>> G=nx.path_graph(4)
>>> h,a=nx.hits(G)
Notes
-----
The eigenvector calculation is done by the power iteration method
and has no guarantee of convergence. The iteration will stop
after max_iter iterations or an error tolerance of
number_of_nodes(G)*tol has been reached.
The HITS algorithm was designed for directed graphs but this
algorithm does not check if the input graph is directed and will
execute on undirected graphs.
References
----------
.. [1] A. Langville and C. Meyer,
"A survey of eigenvector methods of web information retrieval."
http://citeseer.ist.psu.edu/713792.html
.. [2] Jon Kleinberg,
Authoritative sources in a hyperlinked environment
Journal of the ACM 46 (5): 604-32, 1999.
doi:10.1145/324133.324140.
http://www.cs.cornell.edu/home/kleinber/auth.pdf.
"""
if type(G) == nx.MultiGraph or type(G) == nx.MultiDiGraph:
raise Exception("hits() not defined for graphs with multiedges.")
if len(G) == 0:
return {},{}
# choose fixed starting vector if not given
if nstart is None:
h=dict.fromkeys(G,1.0/G.number_of_nodes())
else:
h=nstart
# normalize starting vector
s=1.0/sum(h.values())
for k in h:
h[k]*=s
i=0
while True: # power iteration: make up to max_iter iterations
hlast=h
h=dict.fromkeys(hlast.keys(),0)
a=dict.fromkeys(hlast.keys(),0)
# this "matrix multiply" looks odd because it is
# doing a left multiply a^T=hlast^T*G
for n in h:
for nbr in G[n]:
a[nbr]+=hlast[n]*G[n][nbr].get('weight',1)
# now multiply h=Ga
for n in h:
for nbr in G[n]:
h[n]+=a[nbr]*G[n][nbr].get('weight',1)
# normalize vector
s=1.0/max(h.values())
for n in h: h[n]*=s
# normalize vector
s=1.0/max(a.values())
for n in a: a[n]*=s
# check convergence, l1 norm
err=sum([abs(h[n]-hlast[n]) for n in h])
if err < tol:
break
if i>max_iter:
raise NetworkXError(\
"HITS: power iteration failed to converge in %d iterations."%(i+1))
i+=1
if normalized:
s = 1.0/sum(a.values())
for n in a:
a[n] *= s
s = 1.0/sum(h.values())
for n in h:
h[n] *= s
return h,a
(责任编辑:最模板) |
HITS算法在Web挖掘中的优化
时间:2016-01-14 16:17来源:未知 作者:最模板 点击:次
本文介绍HITS算法在Web挖掘中的优化与改进。 一、HITS算法的基本思想 HITS算法是一种Web结构挖掘,通过挖掘Web链接结构,分析Web间的链接关系,找出Web集合中的authorities和hubs。Authorities是那些
顶一下
(0)
0%
踩一下
(0)
0%
------分隔线----------------------------
- 上一篇:Python垃圾回收机制详解
- 下一篇:fabric实现远程操作和部署
- 热点内容
-
- 高德软件有限公司python试题及答案
1. 在python中, list, tuple, dict, set有什么区别, 主要应用在什么样的...
- Python文件操作函数简介
Python脚本在自动化测试程序中应用很广。本文用实际的代码演示...
- 用Python创建Excel高级工作表
引言 我已写过多篇文章介绍如何使用 Python 和 Pandas 操作数据得...
- Python垃圾回收机制详解
一.垃圾回收机制 Python中的垃圾回收是以引用计数为主,分代收...
- 使用pudb调试python
用于讲解如何使用pudb进行python调试; 1.安装 sudo pip install pudb ...
- 高德软件有限公司python试题及答案
- 随机模板
-
-
 ecshop多属性库存二次开发
人气:4442
ecshop多属性库存二次开发
人气:4442
-
 Magento时尚餐厅主题模板
人气:268
Magento时尚餐厅主题模板
人气:268
-
 电子数码工业化工用品程
人气:979
电子数码工业化工用品程
人气:979
-
 ecshop仿一号店2013最新免费
人气:9180
ecshop仿一号店2013最新免费
人气:9180
-
 ecshop汽车配件类外贸模板
人气:1826
ecshop汽车配件类外贸模板
人气:1826
-
 shopex仿爱情鸟模板
人气:425
shopex仿爱情鸟模板
人气:425
-